Classification Models - Support Vector Machines
Description
Support Vector Machines (SVMs) are a type of machine learning algorithm used for classification tasks. They are based on the concept of finding an optimal hyperplane that separates data into different classes.
SVMs are effective in handling high-dimensional data and can handle both linearly separable and non-linearly separable data by using a technique called the kernel trick. This technique allows SVMs to transform the data into a higher-dimensional feature space, where it becomes linearly separable.
The main objective of SVMs is to maximize the margin, which is the distance between the hyperplane and the closest data points of each class. By maximizing the margin, SVMs can improve their generalization ability and make better predictions on unseen data.
SVMs also have the capability to handle outliers effectively as they primarily rely on the support vectors, which are the data points closest to the decision boundary. These support vectors play a crucial role in defining the hyperplane and are not influenced by outliers.
Overall, SVMs are a popular choice in machine learning due to their versatility, theoretical grounding, and ability to handle complex classification tasks. They have been successfully applied in various domains such as image recognition, text categorization, and bioinformatics.
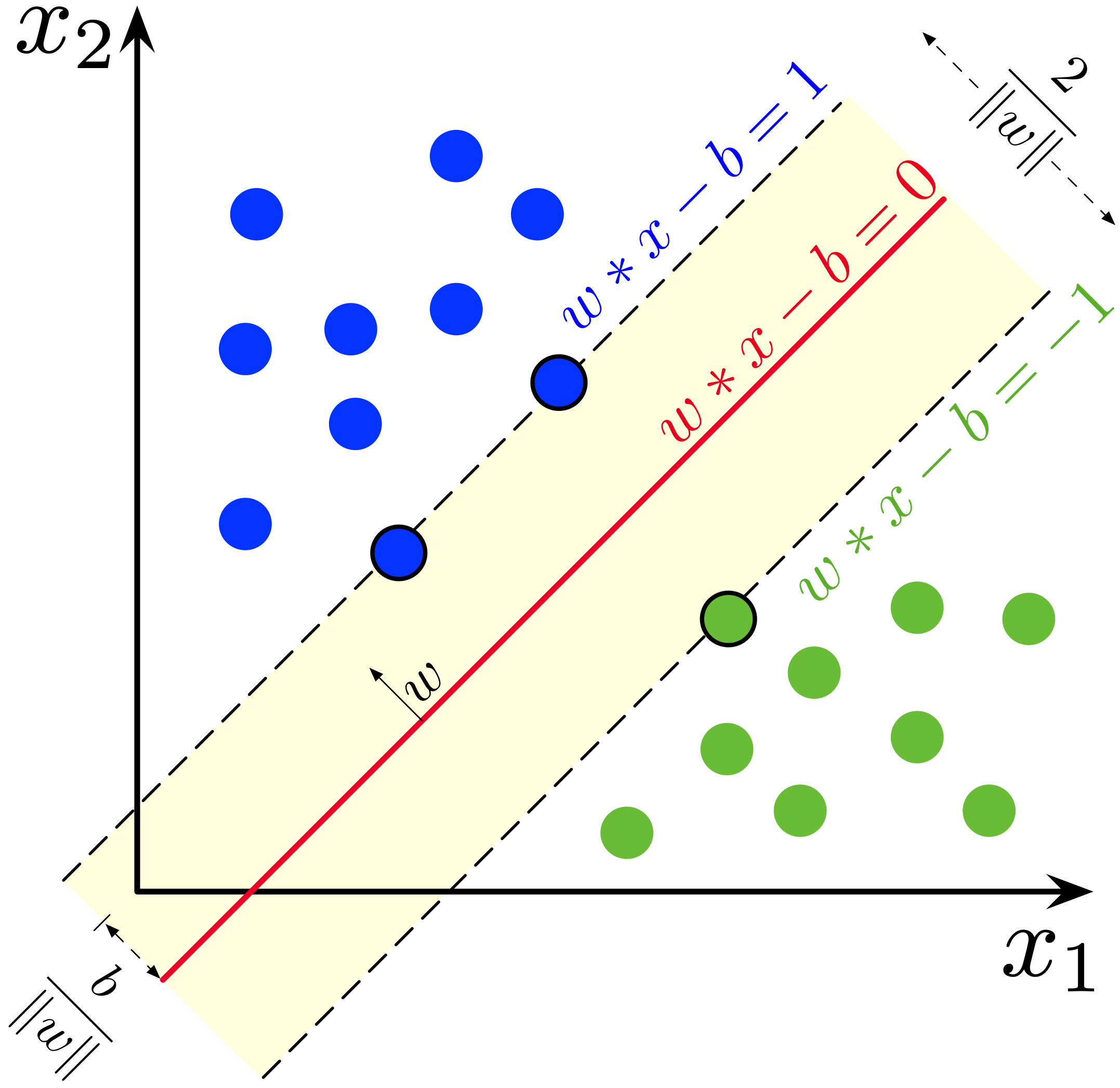

History
Support Vector Machines (SVMs) are a type of supervised machine learning algorithm used for classification tasks. They were first introduced in the 1960s by Vapnik and Chervonenkis in the context of statistical learning theory. SVMs gained popularity in the 1990s when Vapnik and Cortes developed a practical algorithm for training them.
Initially, SVMs were primarily used for binary classification problems. They distinguish data points by finding the hyperplane that maximally separates the classes. In the early 2000s, SVMs were extended to handle multi-class classification tasks using techniques like one-vs-rest and one-vs-one.
SVMs are particularly effective in high-dimensional spaces and can handle both linear and non-linear data by using kernel functions. This allows SVMs to map the data into a higher-dimensional feature space, where linear separation becomes possible.
Since their inception, SVMs have found numerous applications in various domains, including image classification, text categorization, and bioinformatics. Despite the rise of more complex algorithms, SVMs remain relevant due to their robustness, versatility, and ability to handle both small and large datasets.
Use Cases
- Image classification: Support Vector Machines (SVM) can be used to classify images based on their visual features, such as colors, textures, or shapes.
- Email spam detection: SVMs can classify emails as spam or non-spam by analyzing the content of the emails, identifying patterns often found in spam messages.
- Disease prediction: SVM algorithms can be trained on medical data to predict whether a person is likely to develop a particular disease based on their symptoms, medical history, and other relevant factors.
- Face recognition: SVMs can be utilized to recognize faces by learning from a set of labeled images and extracting facial features for classification.
- Document categorization: SVMs can group documents into predefined categories, such as news articles, research papers, or blog posts, based on their content and features.
- Credit risk assessment: SVM algorithms can assess the credit risk of individuals or businesses by analyzing various financial factors to predict the likelihood of default or bankruptcy.
- Fraud detection: SVMs can be used to identify fraudulent transactions or activities by analyzing patterns and anomalies in financial data, helping to prevent fraudulent activities.
- Sentiment analysis: SVMs can classify text data, such as customer reviews or social media posts, into positive or negative sentiments, providing insights into public opinion about products, services, or events.
- Stock price prediction: SVM algorithms trained on historical stock market data can predict future prices based on various financial indicators, assisting investors in making informed decisions.
- Handwriting recognition: SVMs can classify handwritten characters or digits by learning from labeled training data, enabling applications like automated form processing or digit recognition.
Pros
- Highly accurate: Support Vector Machines (SVMs) are known for their high accuracy in classification tasks. They effectively separate data points into different classes, making them suitable for various applications.
- Effective in high-dimensional spaces: SVMs perform well even when the number of features is larger than the number of samples. They can handle complex data easily, making them suitable for tasks with a large number of variables.
- Robust to outliers: SVMs are less sensitive to outliers compared to other classification models. They focus on the support vectors closest to the decision boundary, reducing the impact of outliers on the overall classification.
- Kernel flexibility: SVMs can use different kernel functions, allowing them to handle data that is not linearly separable in the original feature space. Kernels enable SVMs to transform the data into a higher-dimensional space where separation is possible.
- Memory efficient: SVMs only need to store a subset of the training data points (support vectors) in memory. This makes them memory-efficient, particularly when dealing with large datasets.
Cons
- High computational complexity: Support Vector Machines (SVMs) can be computationally expensive, especially when dealing with large datasets. This is because the training time complexity of SVMs is roughly quadratic in the number of training examples.
- Sensitivity to noisy data: SVMs are highly sensitive to noisy data and outliers. These can significantly affect the decision boundary and lead to poor classification results.
- Difficult to interpret: SVM models can be difficult to interpret and provide insights into the underlying relationships between features. Unlike simpler models like decision trees or linear regression, the decision boundary of an SVM model is not easily explainable.
- Selection of appropriate kernel functions: Choosing the right kernel function for an SVM can be challenging. Different types of data and problem domains may require different kernel functions, and the selection process requires expertise and experimentation.
- Memory intensive: SVM models require significant memory resources, especially when dealing with large datasets. The training process requires storing all support vectors in memory, which can become an issue when memory is limited.
Hyper parameters
- Kernel: Specifies the type of kernel function to be used. Options include linear, polynomial, radial basis function (RBF), sigmoid, etc.
- C: Penalty parameter that controls the trade-off between achieving a low training error and minimizing the complexity of the decision function.
- Gamma: Parameter used in the RBF kernel that determines the influence of each training example. Higher values result in a tighter decision boundary.
- Class weights: Assigns different weights to different classes to address class imbalance issues.
- Tolerance: Specifies the stopping criterion for the optimization solver.
- Max iterations: Maximum number of iterations allowed for the solver to converge.
Pitfalls
- Overfitting: Support Vector Machines (SVMs) can be prone to overfitting in situations with a large number of features or when the dataset is noisy. Regularization techniques such as parameter tuning or using kernel functions can help mitigate this issue.
- Choice of kernel: The choice of kernel function in SVMs is crucial and can greatly impact the model's performance. It is important to carefully select an appropriate kernel that suits the problem at hand and the data distribution.
- Sensitivity to parameter tuning: SVMs have various hyperparameters that need to be tuned for optimal performance. Poor selection of these parameters can lead to suboptimal results. Grid search or cross-validation techniques can be used to find the best combination of parameters.
- Large-scale datasets: SVMs can be computationally expensive, particularly when dealing with large-scale datasets. Training time can increase significantly, making SVMs less efficient for big data problems. One approach to mitigate this issue is to use a subset of the data or employ approximate SVM algorithms.
- Imbalanced datasets: SVMs may struggle when applied to imbalanced datasets, where one class significantly outnumbers the other. In such cases, the model tends to favor the majority class and performs poorly on the minority class. Techniques like oversampling the minority class or adjusting class weights can address this issue.
- Lack of interpretability: SVMs do not provide clear explanations for their predictions, making it difficult to interpret the model's decision-making process. This lack of interpretability may be a drawback for certain applications where understanding the model's logic is important.
Algorithm behind the scenes
Sure! Here's a detailed explanation of how Support Vector Machines (SVMs) work in the context of machine learning Classification Models. Support Vector Machines (SVMs) are supervised learning algorithms that can be used for both classification and regression tasks. In this explanation, we will focus on SVMs for classification. SVMs aim to find an optimal hyperplane that separates the different classes of data points in feature space. The hyperplane is a decision boundary that maximizes the distance (margin) between the closest data points from each class, known as support vectors. The inner workings of SVM can be divided into several steps: 1. Data Representation: - Each data point in the dataset is represented as a feature vector. - Feature vectors consist of multiple features or attributes that capture the characteristics of the data. 2. Feature Transformation (optional): - Sometimes it's necessary to transform the original features into a higher-dimensional space. - This transformation allows the data to be linearly separable in the new feature space, even if it wasn't in the original space. - A commonly used technique for this transformation is the kernel trick. 3. Optimization Objective: - SVMs aim to find the optimal hyperplane that maximizes the margin while minimizing the classification error. - The margin is the distance between the hyperplane and the closest support vectors. 4. Margins and Support Vectors: - The points closest to the hyperplane are known as support vectors. - The margin is defined as the distance between the hyperplane and the support vectors. - SVMs maximize this margin during training, as a wider margin generally leads to better generalization. 5. Mathematical Formulation: - The mathematical formulation of the hyperplane is based on a linear equation of the form: w^T * x + b = 0. - Here, w is the weight vector associated with the hyperplane and b is the bias term. - The goal is to find the optimal values for w and b that define the decision boundary. 6. Training and Optimization: - During training, the SVM algorithm solves an optimization problem to find the optimal values for w and b. - This is typically done using an optimization algorithm such as Sequential Minimal Optimization (SMO) or the Primal-Dual method. - The optimization problem involves minimizing an objective function while satisfying constraints related to the margin and misclassifications. 7. Kernel Trick: - The kernel trick allows SVMs to efficiently handle non-linearly separable data. - It involves implicitly mapping the input data into a higher-dimensional feature space using a kernel function. - This mapping allows SVMs to find linear decision boundaries in the transformed space, corresponding to non-linear boundaries in the original space. These steps summarize the general inner workings of Support Vector Machines for classification tasks. The specific mathematical formulations and optimization details can be quite intricate and depend on the specific type of SVM and kernel function used. To visualize the formulas, you can use the website https://latex.codecogs.com by entering the LaTeX code of the formulas and generating images to embed in HTML paragraphs.Python Libraries
Code
Sure! Here are some code samples using the Support Vector Machines (SVM) algorithm for classification models in popular Python libraries: 1. scikit-learn: ```python from sklearn import svm # Create a SVM classifier using linear kernel clf = svm.SVC(kernel='linear') # Train the model clf.fit(X_train, y_train) # Predict class labels for test set y_pred = clf.predict(X_test) ``` 2. TensorFlow: ```python import tensorflow as tf from sklearn import datasets # Load the iris dataset iris = datasets.load_iris() X = iris.data[:, :2] y = iris.target # Create a SVM classifier using TensorFlow model = tf.keras.models.Sequential([ tf.keras.layers.Dense(1) ]) model.add(svm.SVC()) # Compile and train the model model.compile(optimizer='adam', loss='hinge') model.fit(X, y, epochs=100) # Predict class labels for test set y_pred = model.predict(X_test) ``` 3. Keras: ```python from keras.models import Sequential from keras.layers import Dense from keras.wrappers.scikit_learn import KerasClassifier from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split # Load the iris dataset iris = load_iris() X = iris.data[:, :2] y = iris.target # Create a SVM classifier using Keras def svm_model(): model = Sequential() model.add(Dense(1)) model.add(svm.SVC()) model.compile(optimizer='adam', loss='hinge') return model # Wrap the classifier and train the model clf = KerasClassifier(build_fn=svm_model, epochs=100) clf.fit(X_train, y_train) # Predict class labels for test set y_pred = clf.predict(X_test) ``` These code snippets provide examples of how to use the SVM algorithm for classification tasks using different Python libraries. Remember to preprocess your data and split it into training and testing sets before using these codes.